《為什麼 E=mc^2》閱讀筆記

家喻戶曉的質能互換公式，卻鮮見有人討論背後的涵義，僅以此文記錄我曾經試圖理解它的努力

Failed

時間和空間

#

如果在一個飛行中的飛機中往前走動10步，15分鐘後再往後走10步，是否能說是回到「原位」呢？對飛機上的人來說也許是，但對地面上的人而言可能就不是了，因此物體的運動與否是取決於所處的虛擬座標空間。如果把虛擬座標系統的中心放在宇宙的中心，是否就能建立絕對空間呢？我們知道星系正以極快的速度朝其他星系的反方向奔跑，且離我們越遠的星系跑得愈快，所以我們仍然無法知道自己的運動方向和速度，也就無法建立絕對的系統。

根據羅素斷言，一個理論如果沒有實驗能夠驗證真偽的話，那麼這個理論就沒有意義了；同樣地，從飛機的例子中，我們無法找到一個方法來觀測絕對速度，也無法證明自己是否處於運動中，那麼是否處於「原位」自然無法判斷，因此，絕對空間（亞里斯多德空間）的概念也就沒有意義。被迫跳脫絕對空間的思維束縛，我們能觀測的就只有相對空間。既然運動與空間是相對的，而運動又是單位時間內物體在空間中移動的距離，那麼時間是否也可能是相對的呢？

光的速度

#

法拉第發現電磁感應，並且提出「場」的概念，場的重要性在於它能跨越空間，馬克思威爾在法拉第去世後，更進一步歸納出一套方程式來總結各種電子學及磁力學現象。馬克思威爾為了使方程式適用法拉第的實驗觀測結果，在方程式裡引入「位移電流」，卻意外發現新的方程式能以波動方程式的方式表達，並預測了電磁波的存在。馬克思威爾方程式更預測電場與磁場的強度比就是波的速度，即299,792,458m/s，令人驚訝的是，這就是光速！由於此速度的計算過程沒有牽涉波源或接受裝置的速度，所以不是相對的，比較像是自然界中的常數。

在十九世紀末，科學家廣泛相信波必須透過介質才能傳送，因此認為光必須藉由以太這種媒介來傳播，但是邁克生－莫雷眾多檢測以太的實驗都得到無效的結果，最終被迫捨棄以太的概念。以一個簡單的例子來比喻，假如一個人在平靜水面的泳速是5000m/s，河流水流速度3000m/s，對河岸上的人來說，此人順流時會是8000m/s，逆流時會是2000m/s。邁克生－莫雷的實驗就類似這個例子，游泳的人就是實驗中的光束，河流代表以太，河岸就是實驗設備，固定在地球上靜止不動。如果宇宙中存在以太，那麼光速應該會發生變化，但最終測得任何時間任何方向上，光速都是相同的。

根據常識，想像一個人以接近光速前進追上一束光，那麼此人看到的光速和我們看到的光速就會不一樣，這與邁克生－莫雷實驗產生矛盾；因此我們只能被迫接受馬克思威爾方程式的正確性：不管我們跑多快，光都會以299,792,458m/s的速度離我們而去。這代表我們永遠無法追上一束光，也暗示我們應該拋棄絕對時間的概念。（光束本身的時間過得比較快？）

時間軸

#

法拉第（電磁感應）→ 馬克思威爾（電磁波）→ 邁克生－莫雷（以太）

狹義相對論

#

在討論E=mc2E=mc^2之前，首先要理解愛因斯坦的觀點，也就是狹義相對論。

第一部分：透過公理來計算結論

#

狹義相對論存在兩個公理：

  1. 馬克思威爾方程式成立，光速永遠保持不變，無論光源或觀察者本身的速度是多少
  2. 遵循伽利略提出的觀點：沒有任何實驗能測量出絕對速度

根據愛因斯坦光鐘與火車的想像實驗，運動中的光鐘需要走較遠的距離，需要更長的時間來完成一個滴答，如果根據馬克斯威爾說的光速不變，那麼時間在不同地方是以不同速度運行，它的快慢取決於觀測者之間的相對速度。因此，絕對時間與恆定光速之間有矛盾。

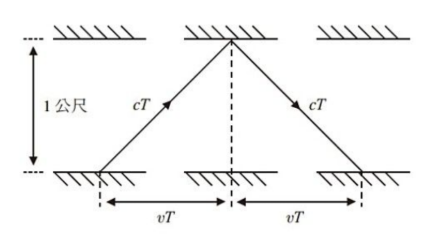
根據光鐘實驗，我們可以進一步推導出相對論中非常重要的一條公式—時間延長性：

γ=11−v2c2\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}

詳細推導過程可參考書中pp.63-66，只需要知道畢氏定理即可理解

第二部分：藉由實驗來驗證

#

布魯克黑文實驗室在20世紀初製造了一架機器，可以發射一束緲子（緲子是一個類似電子的基本粒子，生命週期只有2.2微秒），並圍繞著14公尺的環形軌道，以99.94%的光速運行。按照常理，2.2微秒只能使緲子繞著軌道轉15圈，但實際上它們轉了超過400圈，生命週期變成29倍，大約比60微秒稍多。如果將實驗結果帶入公式，可以發現與理論吻合：

γ=11−v2c2=11−0.99942=10.0346358196091849≈28.87\begin{aligned} \gamma &= \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} \\ &= \frac{1}{\sqrt{1 - 0.9994^2}} \\ &= \frac{1}{0.0346358196091849} \\ &\approx 28.87 \end{aligned}

以上只是從觀察者的角度來看，換成運動者的角度來思考，如果我們和緲子一起環繞軌道，這表示2.2微秒內一共繞了400圈，乍聽之下會覺得奇怪，但其實是因為軌道的周長是會縮短的，而且縮短的程度與緲子生命週期被延長的程度正好一樣。換言之，空間也具有延展性，當物體移動時會變小！

時空

#

p77
愛因斯坦理論的三個核心：不變性、因果性、距離

p83
不變性：假設時間和空間可以合而為一變成一個整體，稱為「時空」，則時空中的距離就是具有不變性的

p84
因果性：起因和結果的先後順序不能反轉，但事件發生間隔足夠遠時，它們之間不存在任何可能的聯繫，這些事件之間的順序是可以顛倒的

p88
測地線：兩點之間的距離

p91
對任意事件，我們都能找到四個獨有的數字來描述它

p92
時間tt與距離xx可以透過校準速度vv進行互換：v=xtv=\frac{x}{t}
天文學中常見的例子就是「光年」，所用的校準速度是光速

p94-95
奧坎剃刀原則：應該先嘗試最簡單的假設，在假設失敗時才逐漸提高複雜程度，直到假設符合實驗結果。
因此假設空間屬於歐幾里得式，已知的測量方法都可以套用至新系統，同時假設時空是不變的，在各處都是一樣的，最終時空中的距離只有兩種可能的計算方式：

  1. s2=(ct)2+x2s^2=(ct)^2+x^2
  2. s2=(ct)2−x2s^2=(ct)^2-x^2

p98-101
ss保持不變的情況下，不同觀測者會得出不同的xx和tt，做出時空圖會發現第一種計算方式（加法畢氏定理）違反因果性，因此只剩下第二種計算方式，也代表歐氏幾何並不適用，於是數學家將適用這條公式計算兩點距離的空間另取了名字，稱為「雙曲空間」，物理學家則稱「閔考斯基時空」

p107
B無法對O造成任何影響，因此事件O和B沒有因果聯繫，沒有違反因果性

p108
45度軸夾住的上下兩區，其中發生的事件與O之間的資訊傳遞速度 < c，左右兩區 > c
c即光速

p115
雙生子矛盾，考慮加速度？

為什麼E=mc2E=mc^2

#

p128-129
第一部分：時空中也可以使用向量，且需要四個數字來描述，稱為「時空速度向量」，向量長度為cc，且被限制在未來光錐中。

p131-132
第二部分：宇宙中存在一個特殊的向量，稱為「動量向量」，不論周遭宇宙發生任何變化，它都不會改變，這個獨一無二的向量是疊加許多其他向量而得到的

p138
移動的事物可以用動量向量來表達
能量守恆定律
因為物理法則對時間具有不變性，所以能量守恆才能實現

p142
基礎方程式必須用存在於時空中的事物來建構，而不是任何只存在空間或時間中的事物

動量這種最基礎的定理，只是存在空間中的箭頭，是否在時空中也適用（具有不變性）？時空中確實存在一個具有不變性的物理量(p143)

p144-146
空間中動量向量的長度可表示為mΔxΔtm\frac{\Delta x}{\Delta t}
則在四維中，根據閔考斯基時空距離的公式，時空中箭頭的長度可表示為(Δs)2=(cΔt)2−(Δx)2(\Delta s)^2=(c\Delta t)^2-(\Delta x)^2
其中只有Δs\Delta s所代表的長度對每個觀測者都一樣（Δt\Delta t和Δx\Delta x都無法滿足這個要求），且光速cc在時空中也不變
假如Δs\Delta s單位是公尺，且光速cc的單位是公尺每秒，則Δsc\frac{\Delta s}{c}的單位為秒（四維的時間段長度）
若將Δx\Delta x替換成Δs\Delta s，將Δt\Delta t替換成Δsc\frac{\Delta s}{c}，即可從三維的ΔxΔt\frac{\Delta x}{\Delta t}推算四維中的速度：

ΔsΔsc=c\frac{\Delta s}{\frac{\Delta s}{c}} = c

我們得到了三維中的動量在四維中對應的量，就是宇宙航速極限cc，一個在時空中運動的事物所擁有的速度大小總是cc，而它的方向取決於事物所運動的方向。新的動量箭頭長度總是mcmc

p148

Δsc=(cΔt)2−(Δx)2c=Δtγ\frac{\Delta s}{c} = \frac{\sqrt{(c\Delta t)^2-(\Delta x)^2}}{c} = \frac{\Delta t}{\gamma}

其中γ=1/1−v2/c2\gamma = 1/\sqrt{1 - v^2/c^2}且v=ΔxΔtv=\frac{\Delta x}{\Delta t}

p149
時空中動量向量在空間方向上的長度為γmv\gamma mv，在時間方向上的長度為γmc\gamma mc

p151-152
由於cc是常數，從所有觀測者的角度來說都不變，因此γmc\gamma mc可視為質量守恆
如果γmc\gamma mc守恆，則γmc2\gamma mc^2亦守恆
對於不超過光速百分之十的速度（v/c=0.1v/c=0.1）的情況，可以用簡化公式估算γ\gamma：

γ=11−v2c2≈1+12v2c2\begin{aligned} \gamma &= \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} \\ &\approx 1 + \frac{1}{2}\frac{v^2}{c^2} \end{aligned}

則

γmc2≈mc2+12mv2\gamma mc^2 \approx mc^2 + \frac{1}{2}mv^2

是守恆的

守恆的能量 = 所有粒子的質量和乘以c2c^2 + 所有粒子的動能和

p159
目前研究光子的人都同意，光子是沒有質量的，那麼運動速度就是cc

為什麼原子、捕鼠夾和星星的能量都值得我們關注？

#

p169
科學知識都只是那些還沒被證明是錯誤的理論和世界觀的集合

質量之源

#

彎曲的時空

#

兩個人從赤道的兩點沿著平行直線往北走，沒有受到外力干擾，最終卻會碰在一起，這是因為地球上任意點都可以假設適用歐式平面幾何，但當這些點組合在一起時，就形成球體而具有彎曲的表面了；同樣地，在時空中，從局部來說任何地方都適用平坦的閔考斯基時空，但將細微的時空塊組合在一起之後，就變成彎曲的時空了。結論就是，由於幾何的原因，萬有引力被剔除了。太陽是具有巨大質量的物體，因此它附近的時空發生彎曲，地球自身其實是在時空中自由地運行著，只是因為太陽周圍的時空發生了彎曲才使地球看上去像在繞圈。

參考資料

#

keyboard_arrow_left返回部落格首頁