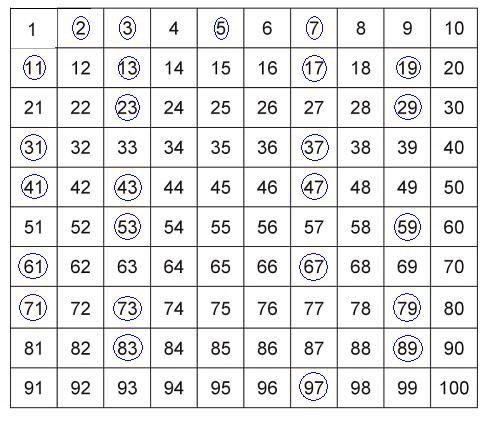
首先直接來看看正規表示式本身：

^1?$|^(11+?)\1+$

仔細看一下可以發現該表示式是由兩個部分組合而成，^1?$ 與 ^(11+?)\1+$，當其中一個部分匹配時則整個表示式成功匹配。

其實，與其說這一串表示式是在尋找質數，不如說它其實是在匹配合數（Composite Number），而且搜尋的對象不是數字本身，而是將數字展開成許多個符號的排列。例如檢查7是否為質數時，其實是將其轉成連續7個1的字串，也就是1111111，然後再透過表示式檢查該字串是否為合數。

翻譯成 Python 的話大約如下：

import re

def is_composite(n: int) -> bool:
    return re.match(r"^1?$|^(11+?)\1+$", "1" * n)

因此如果要檢查是否為質數，只要把是否為合數的結果反轉即可：

def is_prime(n: int) -> bool:
    return not is_composite(n)

順手寫一下單元測試，驗證這一段表示式的功能性：

def test_is_prime():
    assert not is_prime(0)
    assert not is_prime(1)
    assert is_prime(2)
    assert is_prime(3)
    assert not is_prime(4)
    assert is_prime(5)
    assert not is_prime(6)  # 2 * 3
    assert is_prime(991)
    assert not is_prime(1001)  # 7 * 11 * 13

使用 pytest 執行：

pytest test_is_prime.py
==================== test session starts =====================
platform darwin -- Python 3.10.2, pytest-7.3.1, pluggy-1.0.0
rootdir: /Users/gocreating
plugins: anyio-3.6.2
collected 1 item

test_is_prime.py .                                      [100%]

===================== 1 passed in 0.01s ======================

拆解

#

符號說明

#

對正規表示式比較陌生的讀者可以複習一下此處使用到的符號：

• ^: 字串開頭
• $: 字串結尾
• ?: 至多匹配一次 Token (0次、1次)
• +: 至少匹配一次 Token (1次、2次、3次、...無限多次)
• \1: 最近一次匹配到的字串

使用 Python 模擬

#

憑空解釋此表示式背後的含義可能無助於理解實作的邏輯，此處我來試著將原始的表示式以 Python 陳述式的方式翻譯及模擬

def is_composite(n: int) -> bool:
    # ^1?$
    def is_left_part_matched(s: str) -> bool:
        return ...

    # ^(11+?)\1+$
    def is_right_part_matched(s: str) -> bool:
        return ...

    s = "1" * n
    return is_left_part_matched(s) or is_right_part_matched(s)

第一部分

#

左半部分的 ^1?$ 字面上相當直觀，只匹配1出現0次及1次的情況，可以理解為 $n=0$ 或 $n=1$ 時皆視 $n$ 為合數：

def is_left_part_matched(s: str) -> bool:
    return len(s) == 0 or len(s) == 1

此部分看來是在檢查特例情況及邊界。

第二部分

#

右半部分的 ^(11+?)\1+$ 可以先看括號內的 11+?，意義上其實是在執行迴圈尋找因數字串，括號右側的 \1+ 則是拿著目前迭代到的因數字串去檢查能否藉由串接多個因數字串而湊出欲比對的字串。

如果湊得出來，則表示目前的因數可以整除 $n$，也就表示 $n$ 是和數。

def is_right_part_matched(s: str) -> bool:
    for factor in range(2, n):
        # ^(11+?)
        captured_group = s[0:factor]
        # \1+
        accumulated_text = captured_group
        while len(accumulated_text) <= len(s):
            # $
            if accumulated_text == s:
                return True
            accumulated_text = f"{accumulated_text}{captured_group}"
    return False

分析與結語

#

雖然 One-liner 總是為人詬病，但是今天介紹的表示式除了簡潔以外，還充分體現了程式化的邏輯思維，有字串處理、有迭代、有演算法（Backtracking），甚至需要意識到正規表示式的完備性，實在不得不佩服原作者設計之巧妙。

雖然本文使用字元 1 當作範例，但理解原理之後，聰明的讀者們也可以自行更換為其他字元（如：^x?$|^(xx+?)\1+$）來達到相同效果！

本文改寫並啟發自 Hacker News #657 看到的原文 A regular expression to check for prime numbersopen_in_new。